Question

6) y=-4 +3Vx+ 3 A) Domain: x 2-3 Range: y 2-4 B) Domain: x 2-3 Range: y 24 C) Domain: x x 4 Range: y 23 D) Domain: x 2 3 Range: y 2-4

Answer 1

We have the following:

`y=-4+3\sqrt[]{x+3}`

The domain is the input values or the values that x can take and the range is the output values or values that y can take,

For the domain, the value of x cannot be such that it makes what is inside the root less than 0, therefore

`\begin{gathered} x+3\ge0 \\ x\ge-3 \\ D=\lbrack-3,\infty) \end{gathered}`

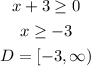
For the range:

Since the second term, the one that contains the root, its minimum value is 0, then the range would be

`\begin{gathered} y\ge-4 \\ R=\lbrack-4,\infty) \end{gathered}`

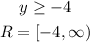
Therefore, the answer is A)