Question

Find the area of the shaded piece. Round to the nearest HUNDREDTH, if needed.AC=24 and m

Answer 1

314.16 square units

Step-by-step explanation

Angles AEB and DEC are vertical angles which means that they are congruent and, therefore, the two shaded areas are congruent as well.

Segment AC is the diameter of the circle because it passes through the center. The radius is half the diameter, AE = EC = 12.

Now, let's find the area of one of the shaded pieces. The area of a portion of a circle of radius r, in an angle θ given in degrees, is,

`A_{one\text{ }shaded\text{ }sector}=(\theta)/(360\degree)\cdot\pi\cdot r^2`

In this case, θ = 125° and r = 12,

`A_{one\text{ }shaded\text{ }sector}=(125\degree)/(360\degree)\cdot\pi\cdot12^2=50\pi\text{ }units^2`

Since both shaded areas are the same, the total shaded area is,

`A=2A_{one\text{ }shaded\text{ }sector}=2\cdot50\pi\text{ }units^2=100\pi\text{ }units^2\approx314.16\text{ }units^2`

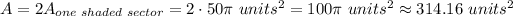
Hence, the area of the shaded piece is 314.16 square units, rounded to the nearest hundredth.