The Solution:
Given the data below:
We are required to find the diameter that represents the 58th percentiles.
Step 1:
We shall re-arrange the given data in ascending order of magnitude.
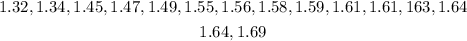
Step 2:
We shall calculate the 58th percentile of the given data.
Note: The diameter that represents the 58th percentile is the diameter in the 58th position when all the given diameters are ranked on a scale of 100.
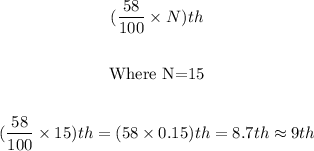
So, the diameter in the 9th position (after rearranging in ascending order) is 1.59.
Therefore, the correct answer is 1.59