Question

The question is 16C I don't understand it, the question is included in the image

Answer 1

The Solution to Question 16C:

Given the functions:

`g(x)=\begin{cases}(x)/(3)+2\text{ if x<1} \\ \\ 4x-2\text{ if x}\ge1\end{cases}`
`f(x)=2x+7_{}`

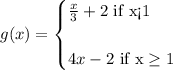
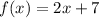
We are required to investigate which of the two functions has the greater average rate of change over the interval

`-12\leq x\leq8`

Step 1:

The formula for the rate of change is:

`\begin{gathered} (f(b)-f(a))/(b-a)\text{ if b>a} \\ \\ a=-12 \\ b=8 \end{gathered}`

Step 2:

We shall find the rate of change for f(x) and g(x).

The rate of change for g(x):

`=((32-2)-(-4+2))/(8+12)=(30--2)/(20)=(32)/(20)=1.6`

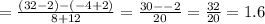
Similarly,

The rate of change for f(x):

`\text{ Rate of change=}(f(8)-f(-12))/(8--12)=(\lbrack2(8)+7\rbrack-\lbrack2(-12)+7\rbrack)/(8+12)`
`=((16+7)-(-24+7))/(20)=(23--17)/(20)=(23+17)/(20)=(40)/(20)=2`

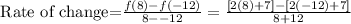
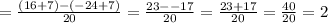
Comparing the rate of change of both functions, we have that:

`\begin{gathered} g(x)\text{ rate of change = 1.6 while that of f(x) =2} \\ \text{ since 2>1.6, we conclude that f(x) has a greater rate of change.} \end{gathered}`

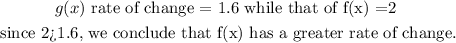
Thus, the function f(x) has a greater average rate of change than the function g(x) since 2 is greater than 1.6 over the given interval.