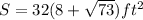Question

Find the surface area of the pyramid. Show work to receive full credit.3 ft16 ft16 ftYou may use the Equation Editor to answer this question. To access the EquationEditor button √x, you may need to select click the Show More Componentsbutton.

Answer 1

Given:

The height of the pyramid is h = 3ft

The base of the pyramid is square.

The side of the square is a =16 ft.

Required:

We need to find the surface area of the pyramid.

Step-by-step explanation:

Consider the surface area of the pyramid formula.

`S=base\text{ area+}(1)/(2)* perimeter* slant\text{ height.}`
`Substitute\text{ base area=a}^2,\text{ perimeter =4a since the base is square. and let slant height =l.}`
`S=a^2\text{+}(1)/(2)*4a* l`

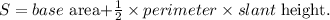
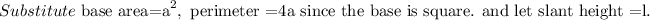
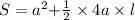
Use the Pythagorean theorem to find the slant height l.

`l=√(3^2+8^2)`
`l=√(9+64)`
`l=√(73)`

`S=a^2\text{+}(1)/(2)*4a* l`
`Substitute\text{ a =16 and l=}√(73)\text{ in the formula.}`
`S=16^2\text{+}(1)/(2)*4(16)*√(73)`
`S=256+32√(73)`
`S=32(8+√(73))ft^2`

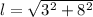
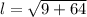
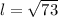
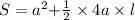
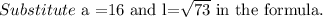
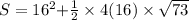
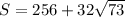
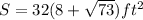
Final answer:

The surface area of the given pyramid is

`S=32(8+√(73))ft^2`