In statistics, a confidence interval is a range of values that is determined through the use of observed data, calculated at the desired confidence level that may contain the true value of the parameter being studied.
The formula to calculate the confidence interval of a sample data is given to be:

where:
CI = confidence interval
x = sample mean
z = confidence level value
s = sample standard deviation
n = sample size
From the question, we have the following parameters provided:

The z-score for a 95% confidence level is gotten to be 1.96.
Therefore, we can calculate the interval to be:
![\begin{gathered} CI=109.33\pm1.96*\frac{12}{\sqrt[]{60}} \\ CI=109.33\pm3.04 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6oxzx57hcth1e7az28fbfn3bl4gny6vmxh.png)
Therefore the interval is between:
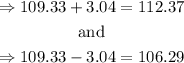
Hence, we are 95% confident that the mean amount spent per dog owner for a single obedience class is between $106.29 and $112.37.