Question

Question 11 When 3x + 2

Answer 1

We are given the following inequality:

`3x+2\le5(x-4)`

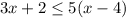
First, we will apply the distributive property on the term on the right side of the inequality:

`3x+2\le5x-20`

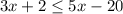
Now we will subtract 5x to both sides:

`\begin{gathered} 3x-5x+2\le-20 \\ -2x+2\le-20 \end{gathered}`

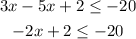
Now we will subtract 2 to both sides:

`\begin{gathered} -2x\le-20-2 \\ -2x\le-22 \end{gathered}`

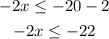
Dividing both sides by -2, since we are dividing by a negative number we need to invert the direction of the inequality sign:

`\begin{gathered} x\ge-(22)/(-2) \\ \\ x\ge11 \end{gathered}`

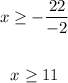
Therefore, the solution is x >= 11