Question

7. A rectangular swimming pool has a length x and a width (x + 6). The swimming pool has an area of 55 meters^2? a. Identify the length and width of the swimming pool.

Answer 1

Length : x

Width : x + 6

Area of a rectangle = length x width

Area = 55 m2

Replacing:

55 = x (x+6)

Solve for x

55 = x^2 + 6x

0 = x^2+6x-55

x^2 +6x - 55

Now we have a quadratic equation, the form is

ax^2 + bx +c

Where:

a= 1

b= 6

c= -55

Apply the quadratic formula:

`\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2\cdot a}`

Replacing:

`\frac{-6\pm\sqrt[]{6^2-4\cdot1\cdot-55}}{2\cdot1}`
`\frac{-6\pm\sqrt[]{36+220}}{2}`
`(-6\pm16)/(2)`

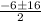
Positive :

(-6+16) /2 = 10/2 = 5

Negative :

(-6-16)/2 = -11

Since lengths and widths can't be negative, we have to use x=5

Width = x+6 = 5+6 = 11

Length = x = 5

Width = 11

Length = 5