Question

In 2011, the moose population in a park was measured to be 5,800. By 2017, the population was measured again to be 8,000. If the population continues to change exponentially, find an equation for the moose population, P, as a function of t, the years since 2011.What does your model from above predict the moose population to be in 2022?

Answer 1

This problem asks to:

a) Find a model to predict the population P as a function of t (years since 2011).

b) Predict the population in 2022.

To find this information, follow the steps below.

Step 1: Write a general equation for populational growth.

The population growth can be represented as:

`P=P_0\cdot e^(r\cdot t)`

Where:

P is the population in time t;

Po is the initial population;

r is the rate of growth;

t is the time.

Step 2: Write the equation that represents the moose population.

Since the problems aks to evaluate the population from 2011. Use the population in 2011 as the initial population.

Then, P0 = 5,800.

`P=5,800\cdot e^(r\cdot t)`

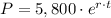
Now, to find r, use the information for 2017.

In 2017,

P = 8,000

t = 6 (2017 - 2011)

Then,

`\begin{gathered} 8,000=5,800\cdot e^(r\cdot6) \\ \end{gathered}`

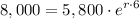
To isolate r, first divide both sides by 5,800:

`\begin{gathered} (8,000)/(5,800)=e^(r\cdot t) \\ (80)/(58)=e^(r\cdot t) \\ \end{gathered}`

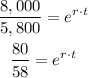
Take the ln from both sides.

`\begin{gathered} \ln ((40)/(29))=\ln e^(6r) \\ \text{ Using the properties of ln:} \\ \ln ((40)/(29))=6r\cdot\ln e \\ \ln ((40)/(29))=6r\cdot1 \\ \ln ((40)/(29))=6r \end{gathered}`

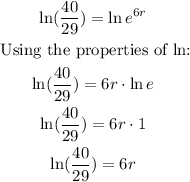
Divide both sides by 6:

`\begin{gathered} (6r)/(6)=(\ln ((40)/(29)))/(6) \\ r=(\ln((40)/(29)))/(6) \\ or \\ r=(0.3216)/(6)=0.0536 \end{gathered}`

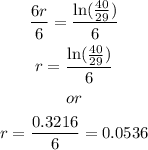
So,

(a) The equation that represents the moose population over the years is:

`P=5,800\cdot e^(0.0536\cdot t)`

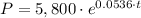
Step 3: Predict the population in 2022.

In 2022,

t = 11 (2022 - 2011).

Then,

`\begin{gathered} P=5,800\cdot e^(0.0536\cdot t) \\ P=5,800\cdot e^(0.0536\cdot11) \\ P=5,800\cdot e^(0.5895) \\ P=5,800\cdot1.8032 \\ P=10,458.6 \\ P=10,459 \end{gathered}`

(b) The moose population in 2022 will be 10,459.

Answer:

(a)

`P=5,800\cdot e^(0.0536\cdot t)`

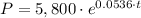
(b) 10,459.