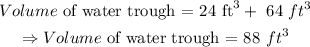Solution:
Given the figure labeled below:
A) Length A and Width B
In the above figure,
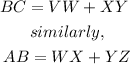


Thus,
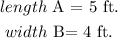
B) The volume of the water trough:
Since the water trough is made up of two rectangular prisms, we can split the figure into two rectangular prisms as shown below:
To calculate the volume,
step 1: Evaluate the volume of prism 1.
The volume of prism 1 is expressed as

step 2: Evaluate the volume of prism 2.
Similarly, the volume of prism 2 is evaluated as

step 3: Sum up the volumes of prisms 1 and 2.
Thus, the volume of the water trough is evaluated to be