Question

The reference angle for 5 is , which has a terminal point of (2,7).What is the terminal point of 5?4O B. (-2,5)O c. (, - )O D. (-2,- 7)

Answer 1

We are asked to determine the endpoints of 5pi/4. The problem can be exemplified in the following diagram:

The x-coordinate of the endpoint is given by:

`x=\cos ((5\pi)/(4))`

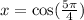
Solving the operations:

`x=-\frac{\sqrt[]{2}}{2}`

The y-coordinate of the endpoint is:

`y=\sin ((5\pi)/(4))`

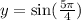
Solving the operation:

`y=-\frac{\sqrt[]{2}}{2}`

Therefore, the endpoint is:

`(-\frac{\sqrt[]{2}}{2},-\frac{\sqrt[]{2}}{2})`