Question

Using the inverse of a matrix solve the following system of equations. Give your answer as an ordered pair.

Answer 1

In order to solve this system using the inverse of a matrix, first let's put the system in the matrix form:

`\begin{gathered} \begin{cases}3x+7y=-4 \\ -x-y=2\end{cases} \\ \begin{bmatrix}{3} & {7} & \\ {-1} & {-1} & {}\end{bmatrix}\cdot\begin{bmatrix}{x} \\ {y}\end{bmatrix}=\begin{bmatrix}{-4} \\ {2}\end{bmatrix} \end{gathered}`

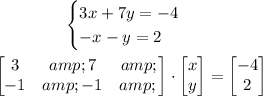
Now the system is in the form AX = B, where A, X and B are matrices.

To solve this system, we can do the following:

`\begin{gathered} AX=B \\ A^(-1)\cdot AX=A^(-1)\cdot B \\ X=A^(-1)\cdot B \end{gathered}`

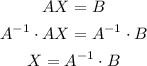
So we need to calculate the inverse matrix of A. We can do this as follows:

`\begin{gathered} A^(-1)=(1)/(|A|)\cdot_{}\begin{bmatrix}{d} & {-b} & \\ {-c} & {a} & {}\end{bmatrix} \\ A=\begin{bmatrix}{3} & {7} & \\ {-1} & {-1} & {}\end{bmatrix}\to a=3,b=7,c=-1,d=-1 \\ |A|=a\cdot d-b\cdot c=-3-(-7)=4 \\ A^(-1)=(1)/(4)\cdot\begin{bmatrix}{-1} & {-7} & \\ {1} & {3} & {}\end{bmatrix}=\begin{bmatrix}{-(1)/(4)} & {-(7)/(4)} & \\ {(1)/(4)} & {(3)/(4)} & {}\end{bmatrix} \end{gathered}`

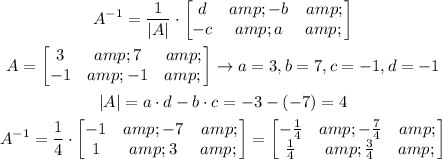
Now we have:

`\begin{gathered} X=A^(-1)\cdot B \\ \begin{bmatrix}{x} \\ {y}\end{bmatrix}=\begin{bmatrix}{-(1)/(4)} & {-(7)/(4)} & \\ {(1)/(4)} & {(3)/(4)} & {}\end{bmatrix}\cdot\begin{bmatrix}{-4} \\ {2}\end{bmatrix} \\ \begin{bmatrix}{x} \\ {y}\end{bmatrix}=\begin{bmatrix}{-(1)/(4)\cdot(-4)+(-(7)/(4))\cdot2} \\ {(1)/(4)\cdot(-4)+(3)/(4)\cdot2}\end{bmatrix}=\begin{bmatrix}{-2.5} \\ {0.5}\end{bmatrix} \end{gathered}`

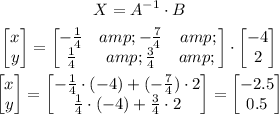
So the solution of this system is x = -2.5 and y = 0.5