Question

A magnet is pushed into a solenoid of 20 coils with a cross-sectional area of 4.0x10-4 m2. As a result, the magnetic field inside the coils changes at a uniform rate from 0.0500 T to 0.180 T in a time interval of 1.90 s.1. What is the magnitude of the emf in [mV] generated in the solenoid?2. If a 5 ohm resistor is connected to the solenoid, what is the magnitude of the current flowing through it in [mA]?

Answer 1

Given:

The number of the coils, N=20

The cross-sectional area of the solenoid, A=4.0×10⁻⁴ m²

The magnetic fields, B₁=0.0500 T

and B₂=0.180 T

The time interval, t=1.90 s

The resistance of the resistor, R=1.90 s

To find:

1. The magnitude of the induced emf.

2. The current flowing through the resistor.

Step-by-step explanation:

1.

The magnitude of the induced emf in the solenoid is given by,

`E=NA((B_2-B_1))/(t)`

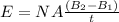
On substituting the known values,

`\begin{gathered} E=20*4.0*10^(-4)*((0.180-0.0500))/(1.90) \\ =0.55*10^(-3)\text{ V} \\ =0.55\text{ mV} \end{gathered}`

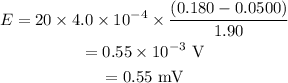
2.

From Ohm's law, The induced emf is given by,

`E=IR`

On substituting the known values,

`\begin{gathered} 0.55*10^(-3)=I*5 \\ \Rightarrow I=(0.55*10^(-3))/(5) \\ =0.11*10^(-3)\text{ A} \\ =0.11\text{ mA} \end{gathered}`

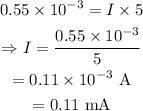
Final answer:

1. The induced emf is 0.55 mV

2. The current through the given resistor is 0.11 mA