We need to find the value of x for the triangle:
Notice that this triangle has a right angle (90º), which is represented by the square marking.
Also, it has two congruent angles, which are represented by the same markings.
Since the internal angles of a triangle must add up to 180º, those acute angles measure 45º each:
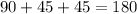
Now, for this 45-45-90 triangle, we have:
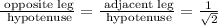
Thus, we have:
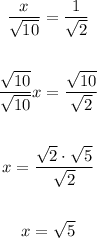
Answer:
