Question

I need help with this question... the correct answer choice

Answer 1

Let us start by writing the coordinates of the parent image and transformed image

Coordinates of the parent image

`\begin{gathered} A\rightarrow(-1,-1) \\ B\rightarrow(-4,0) \\ C\rightarrow(2,2) \end{gathered}`

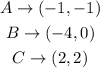
Coordinates of the transformed image

`\begin{gathered} A^(\prime)\rightarrow(1,-1) \\ B^(\prime)\rightarrow(4,0) \\ C^(\prime)\rightarrow(-2,2) \end{gathered}`

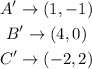
From the coordinates of the parent image and the transformed image collated above, we can conclude that the x-axis of the parent image was multiplied by (-) negative sign while the y-values remaining constant.

The mathematical representation is,

`(-x,y)`

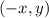
Checking for confirmation

`\begin{gathered} A\rightarrow(-(-1),-1)\rightarrow(1,-1)\rightarrow A^(\prime) \\ B\rightarrow(-(-4),0)\rightarrow(4,0)\rightarrow B^(\prime) \\ C\rightarrow(-(2),2)\rightarrow(-2,2)\rightarrow C^(\prime) \end{gathered}`

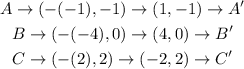
Therefore, the rule that satisfies the transformation is a reflection across the y-axis.

The correct option is Option 5.