Question

Approximate the area under the graph of f(x) over the specified interval by dividing the interval into the indicated number of subintervals and using the left endpoint of each subinterval. f(x)=x^3+x^2+1; interval [0,4]; 4 subintervals

Answer 1

Hello there. To solve this question, we'll have to remember some properties about Riemann sums.

When approximating the area under the graph of a function, we can make a partition of the interval in regular sub-intervals (that divides the former interval in smaller intervals with the same length) and add the areas of the polygons under the graph.

Usually, taking the left endpoint can lead to an under or overestimation, depending on the behavior of the function over the interval (if it is increasing or decreasing, respectively).

So, when approximating the area under the graph of the function f(x) over the interval [a, b], we're partitioning the interval [a, b] into n regular subintervals with length:

`(b-a)/(n)`

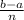
This is also called the forward difference between two points in the endpoints of the interval, also known as:

`\Delta x`

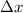
When taking the left endpoints, we start on x = a and will add it up to

`a+(n-1)\Delta x`

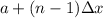
In other words, we'll add all x_i values inside the interval as follows:

`\sum_(i=0)^(n-1)f(x_i)\cdot\Delta x`

Where:

`x_0=a`

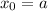
Okay. With this, we can solve the question.

We want to estimate the area under the graph of the function:

`f(x)=x^3+x^2+1`

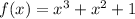
over the interval

`[0,4\rbrack`

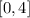
using 4 subintervals (that is, n = 4).

First, we find a and b:

From the interval, we get

`a=0,b=4`

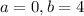
Calculating the difference:

`\Delta x=(4-0)/(4)=(4)/(4)=1`

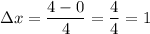
Finally, plugging these informations in the sum:

`\sum_(i=0)^(4-1)f(x_i)\cdot1=\sum_(i=0)^3{x_i}^3+{x_i}^2+1`

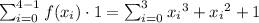
Remember, in this case:

`\begin{gathered} \Delta x=x_1-x_0=1 \\ \text{ but }x_0=a=0,\text{ hence} \\ \\ x_1=1 \\ x_2=2\text{ and} \\ x_3=3 \end{gathered}`

So we get:

`\sum_(i=0)^3{x_i}^3+{x_i}^2+1=1+1^3+1^2+1+2^3+2^2+1+3^3+3^2+1=1+1+1+8+4+1+27+9+1=54`

This might be the approximate area under this graph.

When we want to find the real area, we take the limit as n goes to infinity (the partition becomes big enough such that the intervals have infinitesimal length), hence:

`\underset{n\rightarrow\infty}{\lim}\sum_(i=0)^(n-1)f(x_i)\cdot\Delta x=\int_a^bf(x)\,\mathrm{d}x`

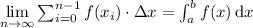
Plugging the function and the lower and upper bounds, we get:

`\int_0^4x^3+x^2+1\,\mathrm{d}x`

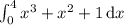
Solving this integral, we get:

`(x^4)/(4)+(x^3)/(3)+x\biggr|_0^4=(4^4)/(4)+(4^3)/(3)+4=64+(64)/(3)+4=(268)/(3)\approx89.34`

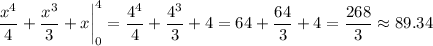
Hence this is why this was a case of underestimation.