Question

given the triangle shown below with exterior angles that measure x°, y°, and z° as shown, what is the sum of x,y,z?

Answer 1

Given:

There are given that the triangle with an interior angle.

Where,

The interior angles are :

`72^(\circ)\text{ and 57}^(\circ)`

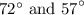
Step-by-step explanation:

To find the value of the addition of x, y, and z, first, we need to draw the reimage.

Then,

The new image is:

Now,

First, we need to find the value of the angle of c.

Then,

From the formula to find the angle c:

`\angle a+\angle b+\angle c=180^(\circ)`

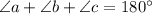
Then,

Put the value of a and b into the above formula:

Then,

Now,

Find all exterior angles x, y, and z.

Then,

First, find the value for x:

`\begin{gathered} \angle x=\angle a+\angle c \\ \angle x=72+51 \\ \angle x=123 \end{gathered}`

Then,

For the values of y:

`\begin{gathered} \angle y=\angle b+\angle c \\ \angle y=57+51 \\ \angle y=108 \end{gathered}`

And,

For the value of z:

Then,

`\begin{gathered} \angle z=\angle a+\angle b \\ \angle z=72+57 \\ \angle z=129 \end{gathered}`

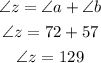
Now,

Add the values of x, y and x:

Then,

`\begin{gathered} x+y+z=123+108+129 \\ =360 \end{gathered}`

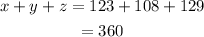
Final answer:

Hence, the correct option is D.