Question

Express each complex number in standard form a+bi:i(a) i^23 (b) 4(3+4i)-5i(1+i)

Answer 1

• (a)-i

,

• (b)17+11i

Explanation:

Part A

We are to express the complex number i²³ in the simplest form.

`\begin{gathered} First\text{ write the index as a sum of an even and an odd number} \\ i^{\mleft\{23\mright\}}=i^(22+1) \\ \text{Next, separate using the addition law of indices} \\ =i^(22)* i^1 \end{gathered}`

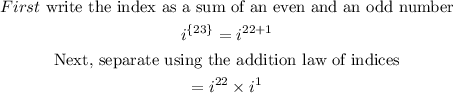
Then rewrite in the form below:

`\begin{gathered} =(i^2)^(11)* i^{} \\ U\sin g\text{ the fact that: }i^2=-1 \\ (i^2)^(11)* i^{}=(-1)^(11)* i=-1* i=-i \end{gathered}`

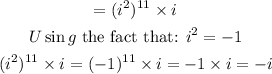
Therefore:

`i^(23)=-i`

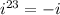
Part B

Given the complex expression:

`4\mleft(3+4i\mright)-5i\mleft(1+i\mright)`

First, open the brackets:

`\begin{gathered} =12+16i-5i-5i^2 \\ =12+11i-5i^2 \\ i^2=-1 \\ \implies=12+11i-5i^2=12+11i-5(-1) \\ =12+11i+5 \\ =12+5+11i \\ =17+11i \end{gathered}`

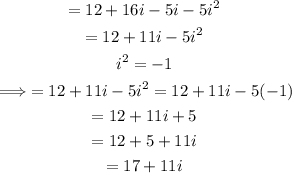
The complex number in standard form is 17+11i.