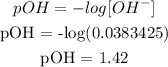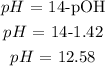Answer:
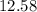
Step-by-step explanation:
We start by getting the number of moles of the acid
We can get that by multiplying the molarity by the volume
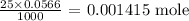
From here, we can get the number of moles of the hydronium ion before the addition of the base
Since the acid is weak, dissociation will be incomplete
We have the dissociation as:
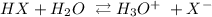
We can get the number of moles of the hydronium ion by the following steps:
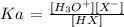
We also have it that:
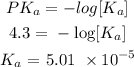
Using an ICE table, we know that the change in the reactant moles is x
Thus, we have it that:
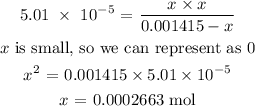
We have the number of moles of hydrogen as x above
Now, we have the pH calculated by subtracting the number of moles of hydroxide ions and dividing by the total volume
We have the hydronium concentration after the addition of the base as follows:
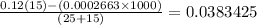
Finally, we can get the pH. What we have from above is pOH since the base is stronger and the acid is weaker. It is expected that what we have is a basic solution.
Mathematically: