Question

Find dy/dx by implicit differentiation. x^3 + y^3 = 8

Answer 1

First, we derivate both sides of the equation to get the following:

`(x^3+y^3=8)^(\prime)=3x^2+3y^2\cdot y^(\prime)=0`

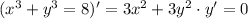
Notice how the derivative of y^3 has to be written: first you do the derivative using the general polynomial formula and then you write y' as a factor.

Then, we just solve for y' to find dy/dx:

`\begin{gathered} 3x^2+3y^2\cdot y^(\prime)=0 \\ \Rightarrow3y^2\cdot y^(\prime)=-3x^2 \\ \Rightarrow y^(\prime)=(-3x^2)/(3y^2)=-(x^2)/(y^2) \\ y^(\prime)=-(x^2)/(y^2) \end{gathered}`

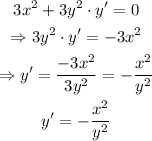
therefore, the implicit derivative of x^3+y^3=8 is y'=-x^2/y^2