Question

age: 33 = 345 bone densityage: 49 = 330 bone densityage: 57 = 325 bone densityage: 65 = 320 bone densityage: 69 = 315 bone density calculate the correlation coefficient, r . round the answer to six decimal places. Is the correlation statistically significant at α = 0.01?

Answer 1

The correlation coefficient is given by the following formula:

`r=\frac{n\sum^{}_{}xy-\sum^{}_{}x\sum^{}_{}y}{\sqrt[]{\lbrack n\sum^{}_{}x^2-(\sum^{}_{}x)^2\rbrack\lbrack n\sum^{}_{}y^2-(\sum^{}_{}y)^2\rbrack}}`

n is the number of samples (5 for this case)

The x values are the ages, while the y values are the bone densities.

We need to build the following table to calculate all the sums of the formula:

xy xy x² y²

33345 113851089119025

49330 161702401108900

57325 185253249105625

65320 208004225102400

69315 21735476199225

The first column has all the ages given, the second has all the values for bone densities. The third column contains the products between the elements in the first and second columns. The fourth contains the square of each x value in the first column, while the last one contains the square of each y value in the second column.

Now, the following table contains the sum of all the values in the columns of the table above.

Σx Σy Σxy Σx² Σy²

2731635 8861515725535175

We can replace now the values of those sums in the formula (and also the n) for calculating the correlation coefficient r:

`r=\frac{5\cdot88615-273\cdot1635}{\sqrt[]{\lbrack5\cdot15725-(273)^2\rbrack\lbrack5\cdot535175-(1635)^2\rbrack}}`

And solving:

`r=-0.995568`

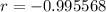
The correlation coefficient for the set of values given is -0.995568.

To determine if the value is statistically significant, we need to know the critical value associated to α = 0.01. This can be found in tables.