Question

A 92-kg rugby player running at 7.5 m/s collides in midair with a 112-kg player moving in the opposite direction. After the collision each player has zero velocity.A. What is the initial momentum of the 92-kg player?B. What is the change in momentum of the 92-kg player due to the collision?Δp1 =C. How is the change in momentum of the 92-kg player related to the change in momentum of the 112-kg player?The two changes in momenta are equal in magnitude and opposite in direction.The two changes in momenta are opposite in magnitude and opposite in direction.The two changes in momenta are equal in magnitude and equal in direction.The two changes in momenta are opposite in magnitude and equal in direction.Part DWhat was the initial speed of the 112-kg player before the collision?Express your answer to three significant figures and include the appropriate units.v2i =

Answer 1

A. pi1 = 690 kg m/s

B. Δp1 = - 690 kg m/s

C. The two changes in momenta are equal in magnitude and opposite in direction.

D. v2i = -6.16 m/s

Step-by-step explanation:

Part A.

The momentum can be calculated as mass times velocity, so the initial momentum of the 92-kg player is equal to

pi = mv

pi = (92 kg)(7.5 m/s)

pi = 690 kg m/s

So, the initial momentum of the 92-kg player was 690 kg m/s

Part B.

After the collision, each player has zero velocity, so the final velocity will be 0 m/s. Then, the change in momentum is equal to

Part C.

In a closed system the momentum is conserved, so to conserve the momentum the change in momentum of the 92-kg player should be equal in magnitude but opposite in direction. Then, when we add them, the sum should be equal to 0. So, the answer is:

The two changes in momenta are equal in magnitude and opposite in direction.

Part D.

Taking into account part C, we can write the following equation

`\begin{gathered} \Delta p_2=-\Delta p_1 \\ m_2v_f-m_2v_(i2)=-\Delta p_1 \end{gathered}`

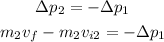
Since the final velocity of the 112-kg player is also 0 m/s, we can solve for v2i as

`\begin{gathered} m_2(0)-m_2v_(2i)=-\Delta p_1 \\ -m_2v_(2i)=-\Delta p_1 \\ v_(2i)=(-\Delta p_1)/(-m_2)=(\Delta p_1)/(m_2) \end{gathered}`

Replacing the values, we get

Therefore, the answers are:

A. pi1 = 690 kg m/s

B. Δp1 = - 690 kg m/s

C. The two changes in momenta are equal in magnitude and opposite in direction.

D. v2i = -6.16 m/s