Question

12. The wheel of a machine rotates at the rate of 300 rpm (rotation per minute). If the diameter of the wheel is 80 cm,what are the angular (in radian per second) and linear speed (in cm per second) of a point on the wheel?

Answer 1

From the question, the wheel of the machine rotates 300 times per minute.

One rotation is 360 degrees.

360 degrees in radians is

`360\degree=2\pi\text{ radians }`

A minute = 60 seconds. So the angular speed w, in radians per seconds become

`w=\frac{300*2\pi}{60\text{ seconds }}=(300*2\pi)/(60)=10\pi\text{ rad/secs}`

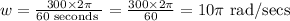
Hence the angular speed is

`10\pi\text{ rads/sec}`

The angular speed w is related to the linear speed v by the formula

`\begin{gathered} v=rw \\ where\text{ v = linear speed = ?} \\ w=angular\text{ speed = 10}\pi\text{ rads/secs} \\ r=radius\text{ =}(diameter)/(2)=(80)/(2)=40\text{ cm } \end{gathered}`

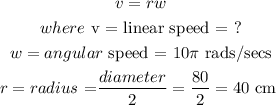
Substituting into the formula, we have

`\begin{gathered} v=rw \\ v=40*10\pi \\ v=400\pi\text{ cm/secs } \\ v=1256.63706\text{ cm/secs } \end{gathered}`

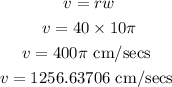
Hence the linear speed is 1256.64 cm/secs to the nearest hundredth