Question

use the quotient property of logarithms to write the logarithm as a difference of logarithms, and simplify if possible:__ -log __

Answer 1

The simplified expression of the logarithm is determined as 4 log 10 - log y.

How to write the difference between the logarithms?

The logarithm as a difference of logarithms, is written by applying the following method as follows;

The given logarithm expression;

`\log (10,000)/(y)`

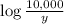
Using the quotient property of logarithm of log a/b = log a - log b, we will have;

`\log (10,000)/(y) = \log 10,000 \ - \log y`

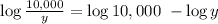
We will simplify the logarithm as follows;

log 10,000 = log 10⁴

= 4 log 10

So the simplified expression of the logarithm becomes;

log 10,000 - log y = 4 log 10 - log y

Answer 2

`\text{ 4}\log _{\{10\}}10\text{ - }\log _{\{10\}}y`Step-by-step explanation:

The quotient property of logarithms states that the logarithm of quotient is the same as the difference of the logarithms

`\log (10,000)/(y)\text{ }`
`\text{Difference of the logarithm = = log}10,000\text{ - log y}`
`\begin{gathered} \log (10,000)/(y)\text{ = log}10,000\text{ - log y} \\ we\text{ can stop here or continue} \\ \text{Since = }log=\log _{\mleft\{10\mright\}} \\ \text{log}10,000\text{ - log y = }\log _{\{10\}}10,000\text{ - }\log _{\{10\}}y \\ =\text{ }\log _{\{10\}}10^4\text{ - }\log _{\{10\}}\text{ y} \\ =\text{ 4}\log _{\{10\}}10\text{ - }\log _{\{10\}}y \end{gathered}`
`\begin{gathered} we\text{ were asked to simplify: } \\ \text{the answer:} \\ \text{ 4}\log _{\{10\}}10\text{ - }\log _{\{10\}}y \end{gathered}`