Question

Solve the system of linear equations. 4x + 4y = -8 ht –2x - 2y = 4

Answer 1

Step-by-step explanation:

We can solve this system by substitution method. It consists in clearing one variable from one of the equations and replacing it into the second equation. This way we'll have one equation for one variable. Once we solve for that variable, we just have to replace it into either of the equations and solve for the other variable.

For this problem we could clear y from the first equation:

`\begin{gathered} 4x+4y=-8 \\ 4y=-4x-8 \\ y=-x-2 \end{gathered}`

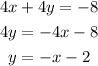
If we clear y from the second equation:

`\begin{gathered} -2x-2y=4 \\ -2y=2x+4 \\ y=-x-2 \end{gathered}`

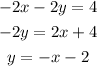
We can see that actually both equations are exactly the same or, in other words, they both represent the same line.

The solution of a system of linear equations represent the point where two lines meet. If two lines are the same they meet everywhere, so there are infinite solutions.

Answer:

Infinite solutions