Question

I would like you to answer these for me with work problem 1 and 2 please

Answer 1

Given the function:

`f(x)=2x^2+4x+1`

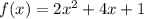
The coefficients of the quadratic equations are:

`\begin{gathered} A=2 \\ B=4 \\ C=1 \end{gathered}`

Where C is the y-intercept, which in this case is 1.

To find the vertex, we can write the vertex form of the equation. Completing squares:

`\begin{gathered} f(x)=2x^2+4x+1=2(x^2+2x)+1 \\ \Rightarrow2(x^2+2x)+1=2(x^2+2x+1-1)+1=2((x+1)^2-1)+1 \\ \Rightarrow f(x)=2(x+1)^2-1 \end{gathered}`

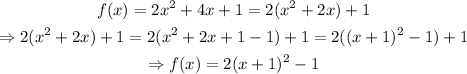
From the generic vertex form of a quadratic equation:

`f(x)=a(x-h)^2+k`

We can identify:

Vertex → (h, k)

If a > 0: The parabola opens up

If a < 0: The parabola opens down

x = h is the equation of the axis of symmetry

From our problem:

`\begin{gathered} a=2 \\ h=-1 \\ k=-1 \end{gathered}`

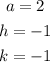
So this parabola opens up, its vertex is at (-1, -1), and the axis of symmetry is

x = -1.

The strategic points are the vertex, the y-intercept, and those values that make f(x) = 0.

`\begin{gathered} 2(x+1)^2-1=0 \\ (x+1)^2=(1)/(2) \\ x+1=\pm\frac{1}{\sqrt[]{2}} \\ x=\pm\frac{1}{\sqrt[]{2}}-1 \end{gathered}`

Then, the two additional strategic points are:

`\begin{gathered} (\frac{1}{\sqrt[]{2}}-1,0) \\ (-\frac{1}{\sqrt[]{2}}-1,0) \end{gathered}`