Question

Office equipment was purchased for $20,000 and is assumed to have a scrap value of $2,000 after 10 years. If its value is depreciated linearly (for tax purpose) from $20,000 to $2,000. (a) Find the linear equation that relates value (V) in dollars to time (t) in years. (b) What is the value of the equipment after 6 years?

Answer 1

According to the information given in the exercise:

- The office equipment was purchased for $20,000.

- The scrap value is assumed to be $2,000 after 10 years.

- -It's depreciated linearly from $20,000 to $2,000.

(a) The Slope-Intercept Form of the equation of a line is:

`y=mx+b`

Where "m" is the slope of the line and "b" is the y-intercept.

Let be "V" the value (in dollars) and "t" the time (in years).

Analyzing the information given in the exercise, you can set up that the equation will have this form:

`V=mt+b`

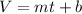
Where "m" is the slope and "b" is the y-intercept.

Notice that you have these two points:

`\begin{gathered} (0,20000) \\ (10,2000) \end{gathered}`

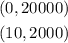
Then, you can apply the formula for calculating the slope:

`m=\frac{y_2-y_1}{x_2-x_1_{}}`

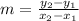
You can say that:

`\begin{gathered} y_2=2000 \\ y_1=20000 \\ x_2=10 \\ x_1=0 \end{gathered}`

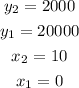
Substituting and evaluating, you get:

`m=(2000-20000)/(10-0)=(-18000)/(10)=-1800`

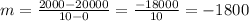
To find "b", you need to remember that the value of "x" is zero when the line intersects the y-axis. Therefore, knowing that one of the points is:

`(0,20000)`

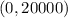
You can determine that:

`b=20000`

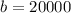
Hence, the equation is:

`V=-1800t+20000`

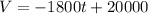
(b) To find the value of the equipment after 6 years, you need to set up that:

`t=6`

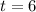
Then, substituting this value into the equation and evaluating, you get:

`\begin{gathered} V=-1800(6)+20000 \\ V=9200 \end{gathered}`

Therefore, the answers are:

(a)

`V=-1800t+20000`

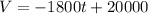
(b) $9,200