Question

Given the normal distribution with mean = 47 and standard deviation = 4, what is the probability that: 1. X<38 or X>45 2. 8% of the values are less than what X value. 3. Between what two X values (symmetrically distributed around the mean) are 85% of the values?

Answer 1

1. Now, we need to get the z-score for

`\begin{gathered} x<38\text{ and } \\ x>45 \end{gathered}`

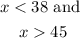
For x < 38, we have

`Z_(38)=(38-47)/(4)=-2.25`

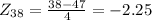
For x > 45, we have

`Z_(45)=(45-47)/(4)=-0.5`

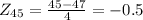
The required probability becomes

`\begin{gathered} Pr(Z<-2.25)\cup Pr(Z>-0.5) \\ \end{gathered}`

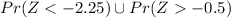
From the Z-score table/calculator, we have that

`\begin{gathered} Z<-2.25=0.012224 \\ Z>-0.5=0.69146 \end{gathered}`

So the union sign/or sign means we add. This becomes

`0.012224+0.69146=0.703684`

Hence the required probability is 0.7037 or 70.37%