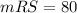You need to remember that there are 360 degrees in a circle. Based on this, you can set up the following equation:
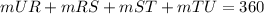
Knowing that:
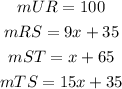
You can substitute the expressions into the equation and solve for "x":
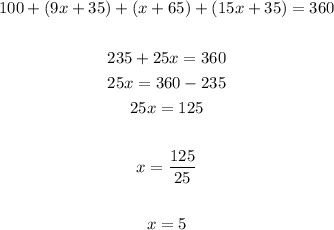
Knowing the value of "x", you can find the measure of RS. This is:
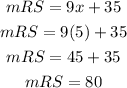
The answer is: