Given equation of lines :
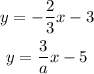
Since the lines are parallel
From the propertoes of parallel lines, the slope of parallel lines are always equal,
where in the general equation of line
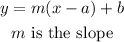
On comapring the the first equation of line with general equation of line
we get m=-2/3
so, slope of first line is -2/3
similarly on comparing second equation of line with the general equation of line,
we get m=3/a
so, slope of second line is 3/a
since slope of both the lines are equal because they are paralle,

So, the value of a is -9/2
Answer : C. -9/2