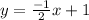The equation of the line is given as,
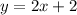
According to the slope-intercept form, the equation of a line with slope 'm' and y-intercept 'c', is given by,
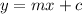
Comparing with the given equation, the slope of the given line is,
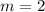
Theorem: The product of two slopes of two perpendicular lines is -1 always.
Let the slope of the perpendicular line be (m'), and 'b' be the y-intercept. Then, it follows that,
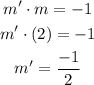
The equation of this perpendicular line is given by,
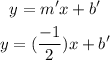
Given that the perpendicular lines pass through the point (6,-2), so it must also satisfy its equation,
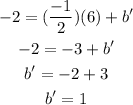
Substitute this value back in the equation of the perpendicular line,
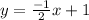
Thus, the equation of a line perpendicular to the given line and passing through the given point is obtained as,