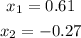
Step-by-step explanation
when you have a quadratic equation in the form:
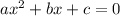
the solution to find x is given by the quadratic formula:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
then
Step 1
reorder the equation, let the zero in the rigth side
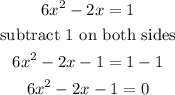
Step 2
identify a, b and c and replace in the formula
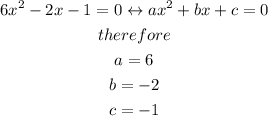
now, replace in the formula.
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x=\frac{-(-2)\pm\sqrt[]{(-2)^2-4(6)(-1)}}{2(6)} \\ x=\frac{+2\pm\sqrt[]{4+24}}{12} \\ x=\frac{+2\pm\sqrt[]{28}}{12} \\ x=\frac{+2\pm\sqrt[]{7\cdot4}}{12} \\ x=\frac{+2\pm2\sqrt[]{7}}{12} \\ x=\frac{1\pm\sqrt[]{7}}{6} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/g1jyyrvkpopp17trcn3vqnq4hzex5bycgk.png)
so, the solutions of the equation are
![\begin{gathered} x_1=\frac{1+\sqrt[]{7}}{6}=(1+2.64)/(6)=0.6076\approx0.61 \\ \text{and} \\ x_2=\frac{1-\sqrt[]{7}}{6}=-0.27429\approx-0.27 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6u3zskxxm7p1ip3jhp2kd05tlozpb7gkcp.png)
I hope this helps you