Answer
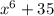
Explanation
A polynomial with one term is called a monomial
A polynomial with two terms is called a binomial
A polynomial with three terms is called a trinomial
In consequence,

Given that we are looking for a binomial, then the first and second choices are discarded.
The degree of a polynomial is the highest exponent of the x-terms. And the leading coefficient is the coefficient (the number) next to the variable with the highest exponent. Therefore,
![\begin{gathered} x^6+35\text{ } \\ \text{ This polynomial has only one x-term, its exponent is 6, the coefficient next to }x^6\text{ is 1 \lparen it is not written\rparen} \\ \text{ Then, it is a 6th degree polynomial with a leading coefficient of 1.} \\ 6x+1 \\ \text{Th}\imaginaryI\text{s polynom}\imaginaryI\text{al has only one x- term, }\imaginaryI\text{ts exponent }\imaginaryI\text{s 1 \lparen it is not written\rparen, the coeff}\imaginaryI\text{c}\imaginaryI\text{ent next to }x\text{ }\imaginaryI\text{s 6} \\ \text{Then, }\imaginaryI\text{t }\imaginaryI\text{s a 1st degree polynom}\imaginaryI\text{al w}\imaginaryI\text{th a lead}\imaginaryI\text{ng coeff}\imaginaryI\text{c}\imaginaryI\text{ent of 6} \end{gathered}]()