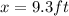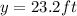Question

I need to know how to solve trigonometric ratios. Need to determine the length for the unknown sides

Answer 1

Given:

AB=9cm, AC=y, BC=z, and the angle ABC = 61.2 degrees.

XZ=21.3ft, XY=x, YZ=y, and the angle XYZ = 66.4 degrees.

Required:

We need to find unknown sides.

Step-by-step explanation:

Consider the triangle ABC.

AB is the hypotenuse, BC is the adjacent side, and AC is the opposite side.

Use sine formula.

`sin\theta=\frac{opposite\text{ side}}{hypotenuse}`
`Substitute\text{ }\theta=61.2\degree\text{ opposite side =y, and hypotenuse = 9cm in the formula.}`
`sin61.2\degree=(y)/(9)`
`y=9sin61.2\degree`
`y=7.9\text{ cm}`

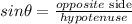
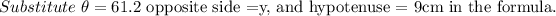
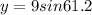
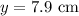
Use the cosine formula.

`cos\theta=\frac{adjacent\text{ side}}{hypotenuse}`
`Substitute\text{ }\theta=61.2\degree\text{ adjacent side =x, and hypotenuse = 9cm in the formula.}`
`cos61.2\degree=(x)/(9)`
`x=9cos61.2\degree`
`x=4.3cm`

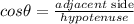
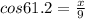
We get x =4.3 cm and y = 7.9 cm.

Consider the triangle XYZ.

YZ is the hypotenuse, XY is the adjacent side, and XZ is the opposite side.

Use sine formula.

`sin\theta=\frac{opposite\text{ side}}{hypotenuse}`
`Substitute\text{ }\theta=66.4\degree\text{ opposite side =21.3, and hypotenuse = y in the formula.}`
`sin66.4=(21.3)/(y)`
`y=(21.3)/(sin66.4)`
`y=23.2ft`

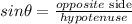
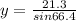
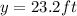
Use the cosine formula.

`cos\theta=\frac{adjacent\text{ side}}{hypotenuse}`
`Substitute\text{ }\theta=66.4\degree\text{ adjacent side =x, and hypotenuse = 23.2 in the formula.}`
`cos66.4\degree=(x)/(23.2)`
`x=23.2cos66.4\degree`
`x=9.3ft`

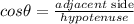
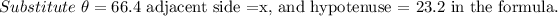
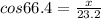
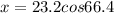
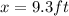
Final answer:

1)

`x=4.3cm`

`y=7.9\text{ cm}`

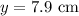
2)

`x=9.3ft`

`y=23.2ft`