The Expected Value of a Discrete Probability Distribution
Given a number of events:
x = {x1, x2, x3,..., xn}
And their respective probabilities:
P = {p1, p2, p3,..., pn}
The expected value is calculated as follows:
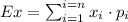
We are given:
x = {-1.25, -0.25, 0, 1.25}
P = {0.1, 0.4, 0.2, 0.3}
Substituting:
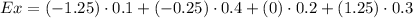
Calculating:
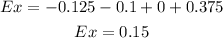
The expected value is $0.15