We need to follow the formula to find the size of the bacterial population is,
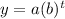
Here, t is the total amount of bacteria, a is the initial bacteria at time = 0, abd b is the growth factor ( which is 2 according to the question )
At t = 110 mins , y = 60,000 we have
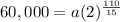
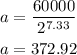
Now, the size of the population after 3 hours
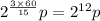
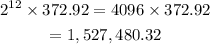
The answer is 1,527,480.32