Let
x be the width
x + 25 be the length
Given that the area is 7154 square feet, then we can substitute the following using the formula for the area of a rectangle

Simplify the left side and equate to zero
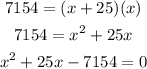
Now it is in the standard quadratic equation with the following coefficients, a = 1, b = 25, and c = -7154.
Use the quadratic formula to solve for x

There are two solutions for x, we will be discarding x = -98, as there is no negative dimensions.
With x = 73, we have the following
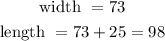
Therefore, the dimensions are 73 feet for width, and 98 feet for length.