Question

A crate of mass m1 = 12.4 kg is pulled by a massless rope up a 36.9° ramp. The rope passes over an ideal pulley and is attached to a hanging crate of mass m2 = 16.3 kg. The crates move 1.60 m, starting from rest. If the frictional force on the sliding crate has magnitude 19.9 N and the tension in the rope is 121.5 N, find the total work done on the sliding crate.what is the total work done on the sliding crate (j)

Answer 1

Given,

The mass m₁=12.4 kg

The angle of inclination of the rope, θ=36.9°

The mass m₂=16.3 kg

The distance through which the crate was moved, d=1.60 m

The friction acting on the sliding crate, f=19.9 N

The tension in the rope, T=121.5 N

The net force acting on the sliding crate is given by,

`F_n=T-f`

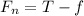
The tension will be pulling the crate up and the friction will be opposing the motion of the crate up the ramp, acting in the downward direction.

The work done is the product of the force applied on an object and the distance through which the object moves.

Thus, work done on the sliding crate is,

`\begin{gathered} W=F_n* d \\ =(T-f)* d \end{gathered}`

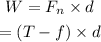
On substituting the known values,

`\begin{gathered} W=(121.5-19.9)*1.60 \\ =162.56\text{ J} \end{gathered}`

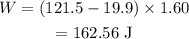
Thus the work done on the sliding crate is 162.56 J