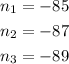Question

find three comsecutive odd integers whose sum is -249 . enter your answers as a coma -seperated list.

Answer 1

Let's call the "smallest" number as n. We know that they're all odd and consecutve, therefore, the second number will be the previous one plus two.

`\begin{gathered} n_1=n \\ n_2=n_1+2=n+2 \\ n_3=n_2+2=(n+2)+2 \end{gathered}`

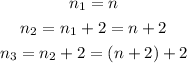
The sum of those three numbers is equal to -249, this gives to us the following equation:

`n+(n+2)+((n+2)+2)=-249`

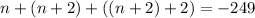
Solving for n, we have:

`\begin{gathered} n+(n+2)+((n+2)+2)=-249 \\ n+n+2+n+2+2=-249 \\ 3n+6=-249 \\ 3n=-249-6 \\ 3n=-255 \\ n=-(255)/(3) \\ n=-85 \end{gathered}`

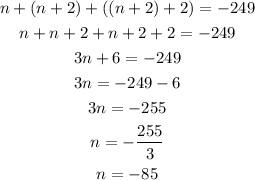
Then, using this value for n, we have our 3 numbers:

`\begin{gathered} n_1=-85 \\ n_2=-87 \\ n_3=-89 \end{gathered}`