To answer this question we will use the following diagram as reference:
From the diagram, we get that, to determine h we can use the trigonometric function tangent:
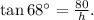
Solving for h, we get:
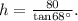
Now, to determine h+x we can do an analogous procedure, therefore:
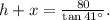
Finally, we get that:
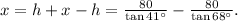
Simplifying the above result, we get:
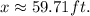
Answer: