Question

A punter kicks the football with an upward velocity of 80 feet per second, The function h(t) = -16t2 + 80t + 2 represents the height of the ball at any given time in seconds. 1. What is the maximum height of the ball? 2. How many seconds will it take the football to reach the maximum height? 3. How long will it take the football to reach the ground?

Answer 1

1) The given function

`h(t)=-16t^2+80t+2`

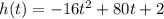
is a quadratic function with a negative leading coefficient, so we can find the maximum value for h(t) by finding the t value for the vertex and use it into the function to find the h value of the vertex.

The formula for the t value of the vertex is:

`\begin{gathered} t=-(b)/(2a) \\ t=-(80)/(2(-16))=-(80)/(-32)=2.5 \end{gathered}`

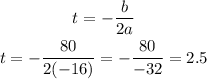
Now, we calculate h(2.5) to get the value for the height:

`\begin{gathered} h(2.5)=-16(2.5)^2+80(2.5)+2 \\ h(2.5)=-16\cdot6.25+200+2 \\ h(2.5)=-100+200+2 \\ h(2.5)=102 \end{gathered}`

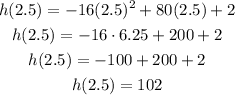
Assuming the height is given in feet, the maximum height is 102 feet.

2) We already calculated this value, since this is the t value of the vertex. Since the time is in seconds, the time it take to reach the maximum is 2.5 seconds.

3) The ground is when the height is equal to zero, so h(t) = 0.

Since this is a quadratic functions, we can use the quadratic formula to calculate this zero:

`\begin{gathered} t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}=\frac{-80\pm\sqrt[]{80^2-4\mleft(-16\mright)\mleft(2\mright)}}{2(-16)} \\ t=\frac{-80\pm\sqrt[]{6400+128}}{-32}=\frac{-80\pm\sqrt[]{6528}}{-32}=(-80\pm80.7960\ldots)/(-32) \\ t_1=(-80+80.7960\ldots)/(-32)=(0.7960\ldots)/(-32)=-0.0248\ldots\approx0 \\ t_2=(-80-80.7960\ldots)/(-32)=(-160.7960\ldots)/(-32)=5.024\ldots\approx5 \end{gathered}`

We have two solutions because there is two moments the ball is on the ground, the initial moment, which is not what we want, and it is at t = 0, first solution, and the moment it goes back to the ground after being kicked, t = 5, which is what we want.

So, it will take approximately 5 seconds for the ball to reach the ground.