SOLUTION:
Step 1:
In this question, we have the following:
Step 2:
a) How many people have contracted the flu after 6 days? We are meant to round our answer to the nearest whole number:
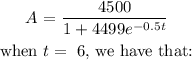
A = 20 people ( to the nearest whole number)
Step 3:
b) What is the carrying capacity of the model?
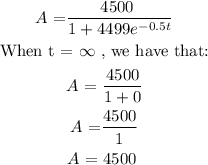
The graph of the carrying capacity is as shown below:
The carrying capacity = 4500
Step 4:
How many days will it take 350 people to contract the flu?
Round the answer to the nearest whole number.
The graph of the solution is as shown below:
From the graph, we can see clearly that when there are 350 people,
it will take:

CONCLUSION: It will take 12 days for 350 people to contract the flu.