the formulam of the volume is
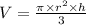
where r is the radius and h the height
r=3/5 because is the half of diameter
h=10
so replacing
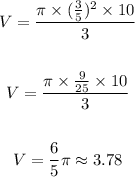
the volume of the cone is 3.78 square millimeters
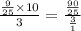
the red multiplication is the numerator and green the denomintor
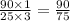
simplify by 15
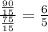
and then add the pi