Answer:
The image below will be able to explain the question
Given:
The diameter of the garden is given below as

The radius of the big circle will be
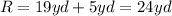
Concept:
To calculate the area of the ring path, we will use the formula below
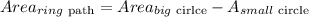
By substituting the values, we will have
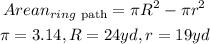
By substituting the values, we will have
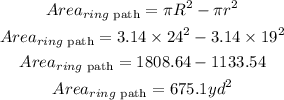
Given in the question
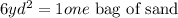
Let the number of bags of sand for 675.1yd² be
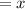
By substituting the values, we will have

Hence,
The final answer is 113 bags of sand