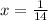Question

Suppose die is weighted such that the probability of rolling a three is the same as rolling a six, the probability of rolling a one, two, or four is 3 times that of a six, and the probability of rolling a five is 3 times that of rolling a three. Find the probability of

Answer 1

Let the probability of rolling a six be x.

Given that the probability of rolling a three is the same as rolling a six.

The probability of rolling a three=x

Given that the probability of rolling a five is 3 times that of rolling a three.

The probability of rolling a five =3x.

Given that the probability of rolling a one, two, or four is 3 times that of a six.

The probability of rolling a one =3x.

The probability of rolling a two =3x.

The probability of rolling a four =3x.

We know that the total probability is 1.

The sum of the probability of one, two, three, four, five, and six =1

`3x+3x+x+3x+3x+x=1`

`14x=1`

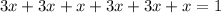
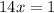
Dividing both sides by 14, we get

`(14x)/(14)=(1)/(14)`

`x=(1)/(14)`

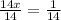
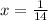
Substitute x=1/14 to get the required probabilities.

The probability of rolling a one is

`3x=3*(1)/(14)=(3)/(14)`

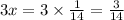
The probability of rolling a two is

`3x=3*(1)/(14)=(3)/(14)`

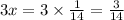
The probability of rolling a three is

`x=(1)/(14)`

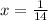
The probability of rolling a four is

`3x=3*(1)/(14)=(3)/(14)`

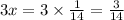
The probability of rolling a five is

`3x=3*(1)/(14)=(3)/(14)`

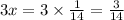
The probability of rolling a six is

`x=(1)/(14)`