Question

Witch function increases at the fastest rate between x=0 and x=8

Answer 1

b. The exponential function f(x) = 2^x + 2

Step-by-step explanation

To find which of these functions increase at the fastest rate we have to find their average rate of change. For the linear functions, this is just the slope of the line. Both equations are written in slope-intercept form,

`f(x)=mx+b`

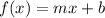
Where m is the slope and b is the y-intercept.

The slope of function f(x) = 2x + 2 is 2, while the slope of function f(x) = 3x + 2 is 3.

For the other two functions, the average rate of change is similar to the slope,

`\text{average rate of change}=(f(a)-f(b))/(a-b)`

a and b are 8 and 0 in this problem. For the exponential function, the average rate of change is,

`(f(8)-f(0))/(8-0)=(258-3)/(8)=(255)/(8)=31.875`

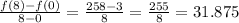
For the quadratic function,

`(f(8)-f(0))/(8-0)=(130-2)/(8)=(128)/(8)=16`

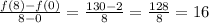
The fastest rate of change is the one with the greatest average rate of change, which in this case is the exponential function.