Question

. Find the area of the unshaded portion of this figure. The figures shown below are a trapezoid and a rhombus 10.1 ft 8.6ft 30.5 ft?

Answer 1

We have to find the unshaded area in the figure.

We can define the unshaded area as the difference between the area of the trapezoid and the area of the rhombus.

The trapezoid has b1=21.4 ft, b2=30.5 ft and h=10.1 ft.

The area can be calculated as:

`A_t=((b_1+b_2))/(2)\cdot h=(21.4+30.5)/(2)\cdot10.1=(51.9)/(2)\cdot10.1=25.95\cdot10.1=262.095\text{ ft}^2`

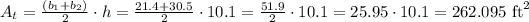
The rhombus has diagonals d1=8.6 ft and d2=h=10.1 ft. Then, the area of the rhombus is:

`A_r=\frac{d^{}_1\cdot d_2}{2}=\frac{8.6\cdot10.1^{}}{2}=(86.86)/(2)=43.43\text{ ft}^2`

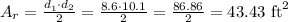
Then, the unshaded area is the difference between At and Ar:

`A=A_t-A_r=262.095-43.43=218.665\text{ ft}^2`

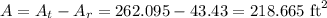
Answer: the unshaded area is 218.665 square feet.