Question

Compound interest4. The price of a flat was £90 000. At the end of each year the price has decreased by 5%.(i) Find the price of the flat after 1 year.(ii) Find the price of the flat after 2 years.

Answer 1

Given

price of a flat was £90 000

decreased by 5%

Find

(i) Find the price of the flat after 1 year.

(ii) Find the price of the flat after 2 years.

Step-by-step explanation

Here we use the formula

`A=P(1-(r)/(100))^t`

i)

`\begin{gathered} A=90,000(1-(5)/(100))^1 \\ \\ A=90,000(0.95) \\ A=85,500 \end{gathered}`

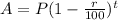
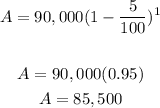
ii) after 2 years ,

`\begin{gathered} A=90,000(1-(5)/(100))^2 \\ \\ A=90,000(0.95)^2 \\ A=81,225 \end{gathered}`

Final Answer

hence ,

i) the price of the flat after 1 year will be £85,500.

ii) the price of the flat after 2 year will be £81,225