1 Answer

Mwoodman · Answer 1 · 2023-07-11T09:29:51+0000

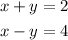
$\begin{gathered} x+y=2 \\ x-y=4 \end{gathered}$

To solve by graphing:

1. Find two points (x,y) for each function:

-First equation:

When x=0

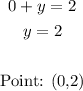
$\begin{gathered} 0+y=2 \\ y=2 \\ \\ \text{Point: (0,2)} \end{gathered}$

When y=0

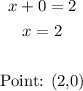
$\begin{gathered} x+0=2 \\ x=2 \\ \\ \text{Point: (2,0)} \end{gathered}$

-Second equation:

When x=0

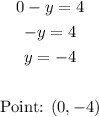
$\begin{gathered} 0-y=4 \\ -y=4 \\ y=-4 \\ \\ \text{Point: }(0,-4) \end{gathered}$

When y=0

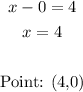
$\begin{gathered} x-0=4 \\ x=4 \\ \\ \text{Point: (4,0)} \end{gathered}$

2. Use the points to graph each function: Put the points in the grind and then draw a line that passes foe each corresponding pair of points:

First function in red

Second function in blue

3. Identify the solution: The solution is the point of intersecion.

Then, the solution is (3,-1)