Let's call x and y as the required numbers.
Their sum is 42, thus:
x + y = 42
Their product is 432, thus:
xy = 432
From the first equation, solve for x:
x = 42 - y
Substitute in the second equation:
(42 - y) y = 432
Multiplying:
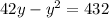
Rearranging:
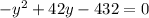
We use the quadratic formula to find the solutions to this equation. For a=-1, b=42, and c=-432:
![y=\frac{-42\pm\sqrt[]{42^2-4\cdot(-1)\cdot(-432)}}{2\cdot(-1)}](https://img.qammunity.org/2023/formulas/mathematics/college/uqo2zkmq8y719efo9igb1npx0oll88fg1a.png)
Calculating:
![\begin{gathered} y=\frac{-42\pm\sqrt[]{1764-1728}}{-2} \\ y=\frac{-42\pm\sqrt[]{36}}{-2} \\ y=(-42\pm6)/(-2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/w510vlyudzbn7amvjybpa9sr804glp2ld2.png)
Separate the two roots:
y = 24 , y = 18
If we use the first value, then x = 42 - 24 = 18
If we use the second value, then x = 42 - 18 = 24
In either case, the two integers are 18 and 24